Применение формулы расчёта простых процентов для вкладов и кредитов

Пример сложного процента на банковском депозите

Удобно и выгодно, когда ваши деньги одномоментно задействованы в разных инструментах. Сразу рекомендую не только у менеджера устно, но и в письменном договоре детально изучить — какой именно процент используется и какие есть нюансы по нему. На некоторых банковских сайтах или в мобильных приложениях есть калькулятор сложных процентов с капитализацией и пополнением. Показываю, как работает эта формула.

1. Первоначальный вклад составил 100 тыс. рублей на 1 год с правом пополнения без ограничения суммы под 5% годовых.
2. Во втором полугодии вы добавили к вкладу еще 100 тыс. рублей.
3. За первую половину вы заработали (100000/100*5%) / 2=2500. Во втором полугодии получили (200000/100*5%) / 2 = 5000. Итого прибыль за год 7500.
4. Далее вы можете забрать свои 7500 или добавить их к 200 тыс. или увеличить вклад еще на определенную сумму.

Наиболее выгодно так работать с проверенными инструментами, поэтапно повышая сумму вклада и внося все данные в excel, чтобы не заблудиться.

 
Как правило, разница на доходе с правом неограниченного пополнения и на обычном способе не превышает 0,5-1% в год, а иногда и вовсе отсутствует.

Ради справедливости нужно рассмотреть и правило, как работает формула расчета простых процентов по кредиту, поскольку ее часто применяют в работе. Простой процент начисляется так: сумма кредита умножается на процентную ставку и поделенная на 365 дней. Для примера: у вас кредит на 100 тыс. рублей под 10% годовых. Если предложен дифференцированный способ, то ежемесячно вам будет начисляться 1000 рублей непосредственно за пользование средствами.

Оплачивая их, через определенный срок можно приступить к погашению самого «тела». Многие банки предлагают аннуитетный платеж, работающий по формуле сложного процента. Это означает, что вы будете оплачивать кредит плюс-минус равными долями. 1000 рублей в месяц за сам кредит и, например, 1000 рублей за само тело. Таким образом, уже на второй месяц проценты будут начисляться на 99 тыс. остатка и с каждым месяцем и платеж по процентам, и выплаты по кредиту будут уменьшаться.

Обратите внимание: сложные проценты по кредиту предлагаются на средних и высоких суммах, в частности, когда оформляете ипотеку или покупаете по договору автомобиль из салона. Хотя есть и аналогичные предложения среди кредитных карт, например, карта Халва, где выплаты подразумеваются равными долями за определенный период и иногда вовсе с минимальными процентами

Узнав способ начисления процента в рабочем инструменте, возможность вносить дополнительно средства или погашать кредит досрочно, важно обратить внимание еще на один аспект — ставку дисконтирования. Это величина, применяемая для пересчета грядущих денежных потоков в общую величину актуальной стоимости. С математической точки зрения, это формула, обратная сложному проценту

С ее помощью оценивается, сколько нужно сейчас инвестировать средств, чтобы, например, через 2 года, получить 100 тысяч. Рассчитывается она по формуле: итоговая сумма (100 тыс. руб) равно как произведение неизвестного на (1+0,1 (10% — средняя ставка банка)), возведенное в квадрат. Далее по правилу пропорции выделите тот самый Х (икс). Фактически, это 82644 рубля

С математической точки зрения, это формула, обратная сложному проценту. С ее помощью оценивается, сколько нужно сейчас инвестировать средств, чтобы, например, через 2 года, получить 100 тысяч. Рассчитывается она по формуле: итоговая сумма (100 тыс. руб) равно как произведение неизвестного на (1+0,1 (10% — средняя ставка банка)), возведенное в квадрат. Далее по правилу пропорции выделите тот самый Х (икс). Фактически, это 82644 рубля.

 
Учитывайте правило: ставка дисконтирования должна быть выше предложенной доходности.

В итоге подчеркну: сложные проценты в финансовых инструментах только на первый взгляд выглядят сложными, но, если разобраться в их сути, никаких камней преткновения не возникнет, а еще более — вы сможете получить существенную выгоду. Всем желаю только выгодных начислений для инвестиций и минимальных для кредита, если же вы все же решились его оформить.

Профессиональный инвестор с опытом работы 5 лет с разными финансовыми инструментами, ведет свой блог и консультирует вкладчиков. Собственные эффективные методики и информационное сопровождение инвестиций.

Что такое сложный процент в инвестициях простыми словами

Знание механизма расчета по депозиту позволяет вкладчикам составить прогноз дохода. Этот расчет доступен при заключении соглашений, выполнении транзакций, перед начислением вознаграждения и капитализацией прибыли.

Банки пользуются простыми и сложными формулами.

При этом применяется фиксированная ставка, которая закрепляется договором при размещении депозита, может регулироваться в случаях:

• автоматической пролонгации договора;
• досрочного закрытия.

Плавающий тип может меняться на протяжении действия соглашения.

Изменение ставок в этом случае привязано к таким факторам:

• курсу валют;
• переводу депозита в другую категорию.

При расчете дохода учитывается ряд показателей:

• инвестиционная сумма;
• процентная ставка, ее тип;
• периодичность начислений;
• срок договора.

При использовании простой схемы расчета итог получается в результате таких математических действий. Начальная сумма умножается на годовую ставку и количество дней начисления вознаграждения и делится на количество дней по календарю и на 100.

Зачем инвестировать под сложный процент

При инвестировании денег рекомендуется выбрать оптимальный вариант, который позволит использовать преимущества сложных ставок. Вложению денег всегда предшествует планирование, анализ поставленной задачи. Капитализация прибыли от инвестирования на счет позволяет получить дополнительный доход.

Простой расчет

Эффективной ставкой считается номинальный процент, который начисляется на сумму с капитализацией. Рассчитать доход можно в программе Excel. Для этого следует ввести исходные данные, формулы на базовый депозит, сумму с капитализацией. Действия выполняются автоматически, поэтому для получения корректного результата рекомендуется внимательно ввести информацию.

Формула

Плата за пользование средствами финансовым учреждением начисляется ежемесячно. Если вкладчик не будет снимать эти средства со счета, то они дополнят сумму основного депозита.

Формула сложного процента записывается: S=X*(1+%)n, где

• S — конечная сумма;
• X — начальный вклад;
• % — годовая ставка;
• n — количество периодов.

В результате прибыль добавляется к сумме и дает доход. Сложный расчет может действовать при открытии срочного депозита.

Выбирая программное предложение банка, нужно ориентироваться на итоговый доход в денежном выражении, который получится при размещении средств.

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби.

• 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
• 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
• 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
• 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
• 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем: 100 — 25 = 75, значит нужно заплатить 75% от первоначальной цены. Используем правило соотношения чисел: 8500 : 4 * 3 = 6375.

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Формула сложных процентов

Формула расчета сложных процентов за год:

Сомрöцнд IнтеREсектзнак равно(п(1+я)п)-пСомрöцнд IнтеREсектзнак равноп((1+я)п-1)жчере:пзнак равноПринсипалязнак равноИнтерест рате ин перцентаге термспзнак равноНумбер оф компоундинг периодс фор а йеар\ begin {align} & \ text {Сложный процент} = \ big (P (1 + i) ^ n \ big) – P \\ & \ text {Сложный процент} = P \ big ((1 + i) ^ n – 1 \ big) \\ & \ textbf {где:} \\ & P = \ text {Принципал} \\ & i = \ text {Процентная ставка в процентах} \\ & n = \ text {Количество периодов начисления сложных процентов для год} \\ \ end {выровнен}Взаимодействие с другими людьмиСложный процентзнак равно( P(1+я)п)-пСложный процентзнак равноP( (1+я)п-1)где:пзнак равноГлавныйязнак равноПроцентная ставка в процентахпзнак равноКоличество периодов начисления сложных процентов за годВзаимодействие с другими людьми

Сложные проценты = Общая сумма основной суммы долга и процентов в будущем (или будущая стоимость ) за вычетом суммы основного долга в настоящее время, называемой  приведенной стоимостью (PV). ТС – это текущая стоимость будущей суммы денег или потока  денежных средств  при заданной  норме прибыли.

Продолжая простой пример с процентами, какова будет сумма процентов, если они начисляются на сложной основе? В этом случае это будет:

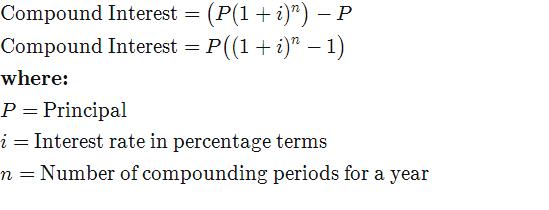
Хотя общая сумма процентов, подлежащих выплате в течение трехлетнего периода по этому займу, составляет 1 576,25 долларов США, в отличие от простых процентов, сумма процентов не одинакова для всех трех лет, поскольку сложные проценты также учитывают накопленные проценты за предыдущие периоды. Проценты, подлежащие выплате в конце каждого года, показаны в таблице ниже.

Проценты: правила

Рассмотрим четыре известных способа поиска процентов.

Занимайтесь математикой в удовольствие вместе с нашими преподавателями на курсах по математике для учеников с 1 по 11 классы!

Нахождение одного процента от числа

При делении на 100% получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать проценты от суммы, нужно умножить их на величину 1%. А чтобы перевести известное значение в проценты, следует разделить его на величину 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Как решаем: Переведем 15% в рубли: 250 : 100 = 2,5 — это 1% от стоимости шоколада, значит, 2,5 × 15 = 37,5 — это 15%. 250 — 37,5 = 212,5. 212,5 < 225.

Ответ: выгоднее воспользоваться скидкой 15%.

Составление пропорции

Пропорция — определенное соотношение частей между собой. 

С помощью метода пропорции можно рассчитать любые проценты. Выглядит это так:

a : b = c : d. 

Читается: а относится к b так, как с относится к d

Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение

Рассмотрим пример. Насколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?

Как решаем: Найдем, сколько рублей составляет выгода, то есть скидка в 14%. Обозначим стоимость футболки за 100%, значит 1390 рублей = 100%. Тогда 14% это х рублей. Получаем пропорцию: 1390 руб. = 100% x руб. = 14% Перемножим крест-накрест и найдем x: x = 1390 × 14 : 100 x = 194,6

Ответ: выгода по скидке составила 194,6 рубля.

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби. Например, 10% — это десятая часть целого. Чтобы найти 10% от числа a, нужно разделить его на 10. Собрали примеры соотношения чисел в таблице.

Процент	Дробь	Как найти % от числа a
10%	1/10	a : 10
20%	1/5	a : 5
25%	1/4	a : 4
50%	1/2	a : 2
75%	3/4	a : 4 × 3

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем: 100% — 25% = 75%, значит, нужно заплатить 75% от первоначальной цены. Используем правило соотношения чисел: 75% — это 3/4 от числа, значит, 8500 : 4 × 3 = 6375 (рублей).

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Расчет процентов по вкладу: формула

Если вы оформляете вклад с простыми процентами (без капитализации), то их легко можно рассчитать по следующей формуле.

Формула расчета процентов по вкладу:

S_п = (S_в*%*N_д)/N_г

где:

• S_п — сумма процентов по вкладу;
• S_в — сумма вклада;
• % — процентная ставка в виде десятичной дроби (например, при 15% годовых, %=0,15);
• N_д — число дней начисления процентов;
• N_г — число дней в году (365 или 366).

Для точного расчета процентов по вкладу нужно точно знать, сколько дней банк будет начислять вам проценты (это указывается в условиях договора). Например, дата зачисления средств может учитываться, а может не учитываться. Дата возврата средств, как правило, не учитывается.

Расчет процентов по вкладу с пополнением и/или снятием производится путем отдельного подсчета для каждого периода нахождения на депозите определенной суммы и суммирования этих результатов.

Рассмотрим, как работает формула расчета процентов по вкладу на примерах.

Схема — простой процент

Схема простых процентов предполагает неизменность базы, с которой происходит начисление.
 

Схема простых процентов используется в практике банковских расчетов при начислении процентов по краткосрочным ссудам со сроком погашения до одного года.
 

Схема простых процентов предполагает неизменность базы, с которой происходит начисление.
 

Схема простых процентов используется в практике банковских расчетов при начислении процентов по краткосрочным ссудам со сроком погашения до одного года.
 

Схема простых процентов предполагает неизменность величины, с которой происходит начисление.
 

Схема простых процентов используется в практике банковских расчетов при начислении процентов по краткосрочным ссудам со сроком погашения до одного года. Длина различных временных интервалов в расчетах может округляться: месяц — 30 дней; квартал — 90 дней; полугодие — 180 дней; год — 360 ( или 365) дней. Другой весьма распространенной операцией краткосрочного характера с использованием формулы простых процентов является операция по учету векселей банком.
 

Схема простых процентов предполагает неизменность базы, с которой происходит начисление.
 

Обычно схема простых процентов используется в практике банковских расчетов для периодов Т 1 года.
 

При начислении процентов по схеме простых процентов одинаково выгодны 1 и 2 варианты, при начислении процентов по схеме сложных процентов более выгоден 1 вариант. Для вкладчика более выгоден 2 вариант.
 

Для кредитора более выгодной является схема простых процентов, если срок ссуды менее одного года ( проценты начисляются однократно в конце периода); более выгодной является схема сложных процентов, если срок ссуды превышает один год ( проценты начисляются ежегодно); обе схемы дают одинаковые результаты при продолжительности периода 1 год и однократном начислении процентов.
 

Таким образом, если денежные средства размещены в банке на срок менее одного года, то более выгодна схема простых процентов. Так, в частности, при сроке в 180 дней наращенная сумма составит: при использовании схемы простых процентов — 1 15 млн руб.; при использовании схемы сложных процентов — 1 1402 млн руб., т.е. получили разницу между суммами в 9 8 тыс. руб. Если срок размещения денежных средств превышает один год, ситуация меняется диаметрально — более выгодна схема сложных процентов, причем наращение в этом случае идет очень быстрыми темпами. Так, при ставке в 30 % годовых при использовании схемы простых процентов за 3 года еще не происходит удвоение исходной суммы, а при использовании схемы сложных процентов за 3 года исходная сумма увеличивается почти в 2 2 раза. Еще большую разницу между наращенными суммами мы видим через 10 лет и тем более через 20 и 50 лет.
 

В банке А вкладчику предложено разместить деньги на депозит на 8 месяцев под 20 % годовых, начисляемых по схеме простых процентов, или на тот же срок, но на условиях начисления 2 % ежемесячно по схеме сложных процентов. Какой вариант размещения денег более выгоден для вкладчика.
 

Инвестиции на условиях простых процентов предполагают начисление очередного процентного дохода только с исходной величины инвестированного капитала, без учета уже начисленных в предыдущие периоды процентов. На практике схема простых процентов используется в банковских расчетах при начислении процентов по краткосрочным ссудам со сроками погашения менее одного года.
 

Какая сумма будет на счете к концу срока, если начисление процентов производится по схеме сложных и простых процентов: а) ежегодно; б) каждые полгода.
 

Таким образом, если денежные средства размещены в банке на срок менее одного года, то более выгодна схема простых процентов. Так, в частности, при сроке в 180 дней наращенная сумма составит: при использовании схемы простых процентов — 1 15 млн руб.; при использовании схемы сложных процентов — 1 1402 млн руб., т.е. получили разницу между суммами в 9 8 тыс. руб. Если срок размещения денежных средств превышает один год, ситуация меняется диаметрально — более выгодна схема сложных процентов, причем наращение в этом случае идет очень быстрыми темпами. Так, при ставке в 30 % годовых при использовании схемы простых процентов за 3 года еще не происходит удвоение исходной суммы, а при использовании схемы сложных процентов за 3 года исходная сумма увеличивается почти в 2 2 раза. Еще большую разницу между наращенными суммами мы видим через 10 лет и тем более через 20 и 50 лет.
 

Деление числа на 100

При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Как решаем: Переведем 15% в рубли: 250 : 100 = 2,5 — это 1% от стоимости шоколада, значит 2,5 * 15 = 37,5 — это 15%. 250 — 37,5 = 212,5. 212,5 < 225.

Ответ: выгоднее воспользоваться скидкой 15%.

Формула сложного процента для банковских вкладов

На самом деле формула сложного процента применительно к банковским вкладам несколько сложнее, чем описана выше. Процентная ставка для вклада (%) рассчитывается так:

% = p * d / y

где p — процентная ставка (процентов годовых / 100) по вкладу, например, если ставка 10,5%, то p = 10,5 / 100 = 0,105; d — период (количество дней), по итогам которого происходит капитализация (начисляются проценты), например, если капитализация ежемесячная, то d = 30 дней если капитализация раз в 3 месяца, то d = 90 дней; y — количество дней в календарном году (365 или 366).

То есть можно рассчитывать процентную ставку для различных периодов вклада.

Формула сложного процента для банковских вкладов выглядит так:

SUM = X * (1 + p*d/y)n

При расчете сложных процентов нужно принимать во внимание тот факт, что со временем наращивание денег превращается в лавину. В этом привлекательность сложных процентов

Представьте себе маленький снежный комок размером с кулак, который начал катиться со снежной горы. Пока комок катится, снег налипает на него со всех сторон и к подножию прилетит огромный снежный камень. Также и со сложным процентом. Поначалу прибавка, создаваемая сложным процентом, почти незаметна. Но через какое-то время она показывает себя во всей красе. Наглядно это можно увидеть на примере ниже.

Калькулятор сложных процентов для вклада

Начальный депозит

Количество периодов

Доходность за 1 период

Довложения каждый период

Расчет сложных процентов: Пример 3. Рассмотрим 2 варианта: 1. Простой процент. Вы инвестировали 50 000 руб на 15 лет под 20%. Дополнительных взносов нет. Всю прибыль вы снимаете. 2. Сложный процент. Вы инвестировали 50 000 руб на 15 лет под 20%. Дополнительных взносов нет. Каждый год проценты прибыли прибавляются к основной сумме.

Начальная сумма: 50 000 рублей
Процентная ставка: 20% годовых
Простой процент	Сложный процент
Сумма	Прибыль за год	Сумма	Прибыль за год
Через 1 год	60 000р.	10 000р.	60 000р.	10 000р.
Через 2 года	70 000р.	10 000р.	72 000р.	12 000р.
Через 3 года	80 000р.	10 000р.	86 400р.	14 400р.
Через 4 года	90 000р.	10 000р.	103 680р.	17 280р.
Через 5 лет	100 000р.	10 000р.	124 416р.	20 736р.
Через 6 лет	110 000р.	10 000р.	149 299р.	24 883р.
Через 7 лет	120 000р.	10 000р.	179 159р.	29 860р.
Через 8 лет	130 000р.	10 000р.	214 991р.	35 832р.
Через 9 лет	140 000р.	10 000р.	257 989р.	42 998р.
Через 10 лет	150 000р.	10 000р.	309 587р.	51 598р.
Через 11 лет	160 000р.	10 000р.	371 504р.	61 917р.
Через 12 лет	170 000р.	10 000р.	445 805р.	74 301р.
Через 13 лет	180 000р.	10 000р.	534 966р.	89 161р.
Через 14 лет	190 000р.	10 000р.	641 959р.	106 993р.
Через 15 лет	200 000р.	10 000р.	770 351р.	128 392р.
Суммарная прибыль:	150 000р.	720 351р.

Комментарии, как говорится, излишни. Вложения с использованием сложного процента НА ПОРЯДОК выгоднее, чем с простым процентом. Чем больше проценты прибыли, чем дольше срок инвестирования, тем ярче проявляет себя сложный процент.

В случае простого процента график увеличения капитала получается линейный, поскольку вы снимаете прибыль и не даёте ей работать и приносить новую прибыль. В случае сложного процента график получается экспоненциальным, с течением времени кривая увеличения капитала становится всё круче, всё больше стремится вверх. Это происходит оттого, что из года в год прибыль накапливается и создаёт новую прибыль.

На графике ниже показано как вырастет капитал, если вложить 50 000 руб на 15 лет под 10%, 15% и 20%.

Как видите, на длительном промежутке времени очень важным становится то, под какой процент вы инвестируете деньги. Через 15 лет при 10% годовых 50 тысяч рублей превратятся в 200 тысяч, при 15% — уже в 400 тысяч, а при 20% годовых — в 780 тысяч.

Таким образом, сложный процент является мощным орудием по увеличению капитала на длительных промежутках времени.

Задачи на проценты с решением

Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.

Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?

Как решаем:

76 : 100 = 0,76 — 1% от массы человека

0,76 * 70 = 53,2

Ответ: масса воды 53,2 кг

Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?

Как решаем:

Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.

х — 0,4х = 0,6x

Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:

0,6х — 0,25 * 0,6x = 0,45x

После двух понижений изменение цены составит:

х — 0,45x = 0,55х

Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.

Ответ: 55%.

Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?

Как решаем:

По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто

100 — 8 = 92

Получается, что стоимость одной пары брюк — это 23% стоимости пальто.

92 : 4 = 23

Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.

23 * 5 = 115

Ответ: пять пар брюк на 15% дороже, чем одно пальто.

Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.

Как решаем:

По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.

Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.

Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.

А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.

Ответ: заработок жены составляет 27%.

Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Как решаем:

Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.

Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.

На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах.

19 : 0,1 = 190

Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.

Формулы простых и сложных процентов

Поскольку простые и сложные проценты чаще всего используются при расчете прибыли от банковских вкладов, продолжим на их примере. Для решения задач нам понадобится такая информация:

• К — начальная сумма вклада;
• К — конечная сумма вклада;
• R — ставка доходности, переводится из процентов в число (10% = 0.1);
• N — количество периодов (лет).

Формула простого процента

По этой формуле мы можем рассчитать конечную сумму вклада без капитализации полученной прибыли. Для этого нужно знать начальную сумму вклада, процентную ставку за 1 период инвестирования и временной интервал. Если конечная сумма задана сразу и нужно найти другую неизвестную переменную, используйте производные формулы простого процента:

Формула сложного процента

По этой формуле мы можем посчитать конечную сумму вклада с учётом капитализации полученной прибыли, зная начальный депозит, процентную ставку и нужный временной интервал. Для решения задач также можно использовать производные формулы сложного процента:

На практике часто дело не заканчивается первоначальным депозитом — многие пользуются регулярными пополнениями, например делают регулярные инвестиции из зарплаты. Для этих случаев формула сложного процента становится длиннее:

где D — сумма регулярных пополнений банковского депозита

Обратите внимание, степень N-1 означает, что доливки начинаются со второго инвестиционного периода (если сумма дополнительных инвестиций вносится сразу, то N-1 меняется на N)

Ну что, удачи на экзаменах всем читающим меня студентам 🙂 Для закрепления далее мы разберем несколько примеров задач на сложные проценты.

Механизм работы

До сих пор мы рассматривали работу сложного процента в теории. Рассмотрим, что они из себя представляют на практике, на примере банковских депозитов и инвестиций.

На примере банковского депозита

При выборе банковского депозита вкладчик должен обращать внимание на несколько параметров: надежность банка, его участие в государственной системе страхования, условия пополнения и снятия денег, минимальная сумма на счете. Но главный из них – процентная ставка и условия ее начисления

Механизм сложных процентов подключен к вкладам с капитализацией процентов. А сама ставка, которая будет действовать на вашем счете, называется эффективной. Если вы не планируете снимать начисленный доход в течение всего срока накопления, то логично выбрать вклад именно с капитализацией.

Сравним полученный доход по депозиту с начислением процентов ежегодно, ежеквартально, ежемесячно и ежедневно. Первоначальные условия:

• сумма – 400 000 ₽;
• % ставка – 4 % годовых;
• срок вклада: 1, 2 и 3 года.

Сумма, которую получит вкладчик в конце срока, составит:

Срок депозита	Начисление процентов
1 раз в год	1 раз в квартал	1 раз в месяц	1 раз в день
1 год	416 000	416 241,6	416 296,62	416 323,38
2 года	432 640	433 142,68	433 257,18	433 312,9
3 года	449 945,6	450 730,01	450 908,75	450 995,73

В инвестициях

Сложный процент работает не только в банковской, но и в инвестиционной сфере. Если в банках процесс начисления процентов на проценты называют капитализацией, то в инвестициях – реинвестированием, т. е. повторным инвестированием. Но суть остается одинаковой.

Долгосрочные инвесторы хорошо знакомы с механизмом сложных % и стараются его использовать по максимуму. Рассмотрим, как он работает в различных инвестиционных инструментах.

Облигации

Доходность облигации складывается из двух источников – рост котировок и купоны. Последние выплачиваются в виде % от номинала ценной бумаги. Как правило, раз в полгода.

Эффект сложного процента можно наблюдать на купонных выплатах, но только в одном случае – если вы полученную прибыль не тратите на текущее потребление, а повторно вкладываете в инвестиции, т. е. реинвестируете. Понятно, что на доход от одной облигации мало что можно купить. Но если ценных бумаг несколько десятков или сотен, то сумма достаточна для покупки еще нескольких облигаций.

Полная информация об актуальных стратегиях, которые уже принесли миллионы пассивного дохода инвесторам

Скачать книгу

Например, владелец одной ОФЗ-26212-ПД 2 раза в год будет получать по 35,15 ₽. За год заработает 70,3 ₽. На эти деньги нельзя купить новую ОФЗ. Если облигаций не одна, а, например, 50 штук, то за год доход составит 3 515 ₽. Можно купить еще 3 ОФЗ за 1 085,81 ₽/шт. (котировка на 27.10.2020).

Если вы не держите облигацию до погашения, а пытаетесь заработать на росте котировок, то и в этом случае полученную прибыль от перепродажи лучше реинвестировать для включения механизма сложных %.

Акции

Точно такой же эффект, как описанный в предыдущем примере, может давать реинвестирование дохода от акций в покупку новых акций. Для этого полученные дивиденды не надо выводить со счета, а повторно инвестировать.

Не все эмитенты выплачивают дивиденды. Некоторые инвесторы покупают в свои инвестиционные портфели акции роста, т. е. бумаги, которые в перспективе могут вырасти в цене. Купил дешевле, продал дороже – одна из стратегий инвестирования. Сложный % заработает, если на полученную прибыль от перепродажи увеличится капитал в инвестициях, а не количество вещей в гардеробе.

Аналогично механизм “снежного кома” работает и с другими инструментами инвестиций. Эффект можно усилить, если инвестировать на ИИС, тогда каждый возврат подоходного налога (максимум 52 000 ₽ в год) необходимо опять возвращать на брокерский счет и покупать ценные бумаги.

Дополнительные параметры и настройки стандартных кредитных алгоритмов

1. Параметры для расчета кредитных продуктов

В программе все платежи учитываются в конце периодов и называются платежами постнумерандо.

Максимальный срок расчета кредитов – 10 лет (120 месяцев).

Заметим, так как шкала времени в Budget-Plan Express 3 года (36 месяцев), все расчеты, после 36-го месяца, относятся к будущему периоду.

В «общих настройках» указываются общие параметры расчета:

1. Шаг расчета (в месяцах, днях);
2. Метод учета годового цикла (ACT/ACT, ACT/360, 360/360);
3. Предельный процент;
4. Расчетный процент (простой, сложный);
5. Расчетная валюта.

Выбирая формулу и условия расчета, можно смоделировать практически любой расчет. К условиям расчета, помимо общих настроек, относятся:

1. Периодичность платежей;
2. Отсрочка по долгу;
3. Отсрочка по процентам;
4. Учет прогрессий;
5. Учет прочих разовых платежей;
6. Учет прочих периодических платежей;
7. Коррекция ставок.

Для нестандартных расчетов можно воспользоваться вкладкой «Таблица платежей«, где можно указать платежи в соответствие с графиком.

2. Платежи, рассчитанные в валюте

Все платежи отображаются в «Таблица платежей» в той валюте, к которой они относятся. При этом на момент выплат, в «Таблица платежей» также рассчитываются расходы (доходы), связанные с курсовыми разницами – в системной (основной) валюте. В тоже время, все расчеты в финансовом плане представлены в системной (основной) валюте. В отчете о прибылях и убытка курсовые разницы отражены в строке (16): «Прочие внереализационные расходы (доходы)» и не включены в «Расходы по обслуживанию долга».

При расчете кредита, например, в долларах, в «финансовом плане» они будут пересчитаны в рубли – по прогнозному курсу.

3. Прогрессивные выплаты долга

Прогрессивные выплаты используются только для «стандартного» кредитного продукта, когда процентные деньги погашаются в зависимости от остатка долга.

• 1. Платежи, изменяющиеся в

арифметической прогрессии:

Z = [2B₁ + d (n-1)] n / 2,

отсюда первая выплата долга:

B₁ = Z / n — d(n-1) / 2

где:
Z – сумма долга,
B₁ – первая выплата долга,
d – разность арифметической прогрессии (сумма).

2. Платежи, изменяющиеся в геометрической прогрессии:

Z = B₁ / ,

отсюда первая выплата долга:

B₁ = Z /

где:
Z – сумма долга,
B₁ – первая выплата долга,
q – знаменатель геометрической прогрессии (процент).

4. Способы определения количества дней

В общепринятой практике существует несколько способов определения срока возврата ссуд t (в годах) для ссуд, выданных на
срок, который исчисляется в днях. В каждом из этих способов срок
возврата ссуды t (в годах) вычисляется по формуле:

t = s / g,

где числа s и g определяются в зависимости от способа расчета:
1. «Английский» способ или ACT/ACT.
Число s равно точному числу дней ссуды минус один день (день
выдачи и день погашения ссуды считаются одним днем), число g равно точному числу дней в году (365 или 366). Этот способ
называется английским и часто упоминается, как способ 365/365
или ACT/ACT.
2. «Французский» способ или ACT/360.
Число s равно точному числу дней ссуды минус один день (день
выдачи и день погашения ссуды считаются одним днем), число
g равно 360 (в году 12 месяцев по 30 дней). Этот способ
называется французским и часто упоминается, как способ
365/360 или ACT/360.
3. «Немецкий» способ или 360/360.
Число g равно 360 (в году 12 месяцев по 30 дней), число s
состоит из полного числа месяцев (по 30 дней) плюс точное
число дней в оставшемся неполном месяце минус один день
(день выдачи и день погашения ссуды считаются одним днем).
Этот способ называется немецким и часто упоминается, как
способ 360/360.

В финансовой практике, чтобы определить точное число дней ссуды t, используют специальные таблицы, в которых указаны порядковые номера даты в стандартном году.
Число дней между датами определяется как разность между номерами этих дат.

В Budget-Plan Express алгоритм определения точного количества дней «зашит» в расчет. Чтобы использовать этот алгоритм, нужно указать шаг расчета в днях (вкладка «настройки»).

5. Метод расчета предельной величины процентов по ставке рефинансирования

Предельный процент – это предельная величина процентов, признаваемых расходом, включая проценты и суммовые разницы по обязательствам. Рассчитывается с учетом ставки рефинансирования: ставка рефинансирования помноженная на коэффициент.
Зависит от налогового законодательства (той или иной страны) в конкретном случае. В некоторых налоговых законодательствах коэффициент может зависеть от валюты кредита. Например, предельная ставка в рублях = ставка рефинансирования * 1,8, предельная ставка в валюте = ставка рефинансирования * 0,8.

Справка о программе «Budget-Plan Express», www.strategic-line.ru | Содержание справки