Сколько можно выиграть на ставках: калькулятор расчета по коэффициенту

Формула простых процентов.

Она используется тогда, когда начисляемый доход присоединяется к основному телу депозита в конце его срока или не присоединяется и выводится на текущий счет или пластиковую карточку. Этот порядок расчета стоит учесть, когда размещается солидная сумма на длительный срок. Обычно в данном случае банки применяют варианты размещения без капитализации, что понижает общую выгоду вкладчика.

Формула простого %:
Сумма % — это  доход, полученный через i-ый промежуток времени.

Р – изначальный объем вложений.

i – депозитная годовая ставка.

t – срок вложения.

T – число дней в году.

Рассмотрим пример: разместим 100 000 рублей на полгода под 12%. Рассчитаем полученный доход:

Таким образом, через полгода со счета можно будет снять 105 950,68 руб.

Как посчитать проценты без калькулятора?

Процент — это буквально одна сотая часть от одного числа или суммы чисел. Высчитать один процент не сложнее, чем сделать график в Ворде: достаточно разделить исходное значение на сто. Ниже будет на примерах показано, как подсчитать процент в разных ситуациях.

Формула для расчёта процентов от числа или суммы имеет вид:

• ХП — искомые проценты;
• Х — количество процентов;
• Ч — исходное число.

Пример 1. Узнать, сколько будет 11% от 80. Расчёты осуществляются в одно действие: 11 × 80 / 100 = 88 / 100 = 8,8.

Пример 2. Вычислить 15% от суммы чисел 17 и 23. Чтобы найти результат без калькулятора, удобно разбить вычисления на три действия:

• 15% × 17 = 15 × 17 / 100 = 2,25 — для первого слагаемого.
• 15% × 23 = 15 × 23 / 100 = 3,45 — для второго слагаемого.
• 2,25 + 3,45 = 5,7 — полученная сумма.

Таким образом, 15% от суммы равно 5,7. Можно и сложить оба числа, а затем посчитать процент от результата — полученное значение будет точно таким же.

Пример 3. Найти, сколько будет 35% от разности чисел 98 и 52. Правильно считать в этом случае можно двумя способами: как в предыдущем, разбив вычисление на три действия, или сразу вычесть из первого числа второе, и узнать процент от разности: 35% × (98 — 52) = 35% × 46 = 35 × 46 / 100 = 16,1.

Пример 4. Вычесть 25% из 28. Чтобы получить результат, нужно:

• Посчитать 25 процентов от 28: 25% × 28 = 25 × 28 / 100 = 7.
• Отнять полученное значение от исходного: 28 – 7 = 21.

Итак, посчитать проценты от числа или суммы можно только одним способом — вывести какую-либо новую формулу пока ещё никому не удалось.

Чтобы облегчить вычисление, можно использовать простое правило. Формулируется оно следующим образом: А процентов от числа Б — это точно то же самое, что Б процентов от числа А. Так, 25% от 80 равно 80% от 25; убедиться в этом можно, проведя простые вычисления:

• 25% × 80 = 25 × 80 / 100 = 20.
• 80% × 25 = 80 × 25 / 100 = 20.

Стандартная формула расчета процентов по кредиту

Для расчета можно использовать данную формулу:

S = [I / 100 / K*T] * P

В данной формуле присутствуют такие переменные:

S – условная сумма, которая определяет точный платеж;

I – процент переплаты за один год;

K — из скольки дней состоит год, по факту (високосный/не високосный);

T – срок выплаты кредита в днях;

P – конечная сумма долга, в день расчета.

В чем состоит расчет процентов по кредиту, формула которого представлена выше?

Для начала, стоит понять, для чего делить процент переплаты на 100. Это делается с целью его перевода в вид дроби. Далее, это дробь нужно поделить на дни в году, чтобы просчитать ставку за один день.

После того как рассчитана ставка в день, нужно рассчитать то, сколько придется переплачивать за весь период, так как он может состоять из нескольких лет или содержать в сроке неполный год.

Для этого нужно умножить ставку по кредиту за один день на общее количество всех дней периода кредитования.

И ту ставку, что получается после этого, нужно умножить на конечную сумму долга. Полученная в итоге сумма является нужным платежом.

Пример второй – Капитализация процентов ежеквартально

Капитализация процентов ежеквартально

Капитализация процентов – ежеквартально. Применяем формулу сложных процентов. Действуем по аналогии с первым примером

Но, обращаю ваше внимание на достаточно распространенную ошибку при расчете. Многие, при расчете ежеквартальной капитализации, подставляют в формулу j – неправильное количество дней

Нужно ставить не 30 или 31 день, по количеству дней в месяце, а количество дней за общий календарный период. Для этого мы суммируем количество дней за 3 месяца каждого квартала.

• В первом квартале – это будет 90, либо 91 день, в зависимости от того, сколько дней в феврале, например: Январь (31 день) + Февраль (28 дней) + Март (31 день) = 90 дней.
• Во втором квартале – это будет 91 день: Апрель (30 дней) + Май (31 день) + Июнь (30 дней) = 91 день.
• Во третьем квартале – это будет 92 дня: Июль (31 день) + Август (31 день) + Сентябрь (30 дней) = 92 дня.
• Во четвертом квартале – это будет 92 дня: Октябрь (31 день) + Ноябрь (30 дней) + Декабрь (31 день) = 92 дня.

1 кв.: S=(100 000 х 14 х 90 / 365) / 100S=3452,05 руб. Прибавляем это к первоначальной сумме. Получаем 103452,05 руб. Дальше по аналогии с первым примером.

Проценты: правила

Рассмотрим четыре известных способа поиска процентов.

Занимайтесь математикой в удовольствие вместе с нашими преподавателями на курсах по математике для учеников с 1 по 11 классы!

Нахождение одного процента от числа

При делении на 100% получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать проценты от суммы, нужно умножить их на величину 1%. А чтобы перевести известное значение в проценты, следует разделить его на величину 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Как решаем: Переведем 15% в рубли: 250 : 100 = 2,5 — это 1% от стоимости шоколада, значит, 2,5 × 15 = 37,5 — это 15%. 250 — 37,5 = 212,5. 212,5 < 225.

Ответ: выгоднее воспользоваться скидкой 15%.

Составление пропорции

Пропорция — определенное соотношение частей между собой. 

С помощью метода пропорции можно рассчитать любые проценты. Выглядит это так:

a : b = c : d. 

Читается: а относится к b так, как с относится к d

Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение

Рассмотрим пример. Насколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?

Как решаем: Найдем, сколько рублей составляет выгода, то есть скидка в 14%. Обозначим стоимость футболки за 100%, значит 1390 рублей = 100%. Тогда 14% это х рублей. Получаем пропорцию: 1390 руб. = 100% x руб. = 14% Перемножим крест-накрест и найдем x: x = 1390 × 14 : 100 x = 194,6

Ответ: выгода по скидке составила 194,6 рубля.

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби. Например, 10% — это десятая часть целого. Чтобы найти 10% от числа a, нужно разделить его на 10. Собрали примеры соотношения чисел в таблице.

Процент	Дробь	Как найти % от числа a
10%	1/10	a : 10
20%	1/5	a : 5
25%	1/4	a : 4
50%	1/2	a : 2
75%	3/4	a : 4 × 3

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем: 100% — 25% = 75%, значит, нужно заплатить 75% от первоначальной цены. Используем правило соотношения чисел: 75% — это 3/4 от числа, значит, 8500 : 4 × 3 = 6375 (рублей).

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Онлайн-калькулятор

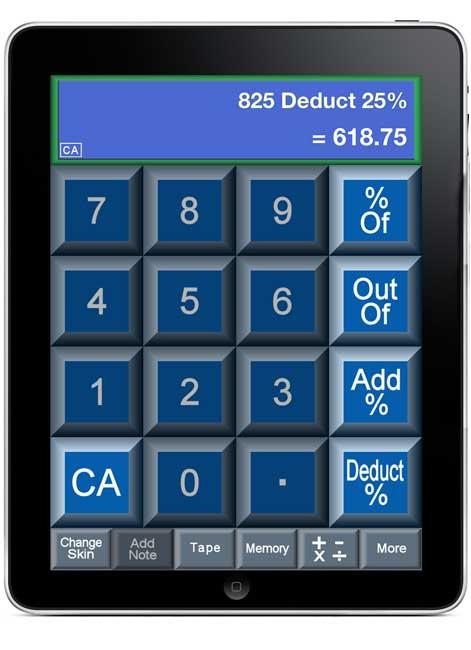
Если вы уже знакомы со всеми правилами и умеете их с легкостью использовать, но ситуация срочная и нужно все быстро посчитать — можно обратиться за помощью к калькулятору. Нахождение ответа выглядит так:

• Для подсчета процента от суммы: вводим известное, равное 100%, знак умножения, нужный процент, знак %.
• Чтобы вычесть проценты: введем известное, равное 100%, знак минус, размер процентной доли и знак %.

Если на уроке в 5 или 6 классе вам нужно проверить правильность нахождения процента от числа, то поможет онлайн-калькулятор. Вот несколько сайтов, к которым можно обратиться:

• раз,
• два,
• три,
• четыре.

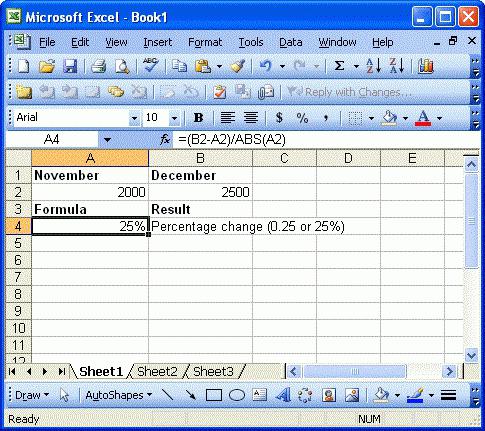
Расчёт процентов в excel

Многие задаются вопросом, как научиться считать проценты в exсel. На самом деле, в этом нет ничего сложного, если вы владеете минимальными базовыми навыками компьютерного пользователя. Программа сделает за вас большую часть работы.

В экселе формула необходимых расчетов задается в зависимости от того, относительно каких процентов необходимо получить результат. Рассмотрим основные и наиболее типичные примеры:

Базовая формула расчета процента: часть / целое = процент

В отличии от привычной математики, здесь не требуется умножение на 100, так как программа делает это сама, при заданном для ячейки процентном формате.

Предлагаю вашему вниманию пошаговую инструкцию вычисления процентов через exel:

1. У нас есть три столбца в программе. Первый столбец «А», второй «В», третий «С».
2. В первом мы пишем число, от которого будем искать процент. Во втором пишем число процентов, обязательно со значком «%». В третьем программа будет выдавать нам результат.
3. Итак, чтобы получить нужный результат в столбике «С», следует набрать в нем знак равенства, затем кликаем на столбик «А», ставим знак умножения, кликаем на столбик «В» и нажимаем enter. Результат готов.

Как быстро высчитать проценты

Иногда бывают случаи, когда нет времени разбираться с формулами или самостоятельно пересчитывать числа. На этот случай в интернете предусмотрены многочисленные онлайн калькуляторы, которые моментально выдадут вам готовый результат. Достаточно всего лишь ввести исходные данные в специальные окошки, и любой пример на калькуляторе будет просчитан автоматическим алгоритмом.

На этом я с вами прощаюсь, дорогие друзья. Надеюсь, изложенные мною советы по расчету процентов так или иначе пригодятся вам в быту или на работе.

Не забывайте делиться этой публикацией в соцсетях, подписываться на мой блог, а также следите за новыми интересными материалами. 

Обратное вычисление

Очень часто в вопросе о том, как посчитать процент от суммы, возникает и недвусмысленный обратный перевод. На практике это связано, скажем, с обратным вычислением четверти. Всем известно, что этот показатель составляет 25% от начального числа. Пусть, например, цену товара увеличили на 25%, что составило 25 рублей. Нужно найти, сколько стал стоить данный товар. Вот теперь попробуем разобраться, как вычислить не первоначальное число, зная значение процента, а всю сумму, которая должна получиться в конечном итоге. Казалось бы, решение простое:

25 = 25% (1/4 или 0,25);

Нет, абсолютно неверно. Так можно получить только изначальное число, без учета 25%. Для расчета всей суммы с учетом 25% нужно использовать формулу:

Или 100/0,8, что и покажет значение 125 (100 + 25), поскольку 100% плюс 25% в выражении единицы является числом 1,25 (единица плюс четвертая часть), а в обратном виде (1/x) – это именно 0,8. Произведя вычисления, получим, что х = 125.

Основные определения

Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.

Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».

Процент — это одна сотая часть от любого числа. Обозначается вот так: %.

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить число на 100, как в примере выше.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:

0,18 = 0,18 · 100% = 18%.

А вот, как перевести проценты в десятичную дробь — обратным действием:

18 : 100 = 0,18.

Выразить дробь в процентах просто. Для перевода сначала превратим её в десятичную дробь, а потом используем предыдущее правило:

Сферы использования

Рассмотрим, в каких ситуациях обычный человек может столкнуться с ключевой ставкой.

Кредиты и вклады

Большинство населения сталкивается со ставкой ЦБ при размещении денег во вкладах и получении кредитов. Вот как происходит влияние:

1. Центробанк не работает напрямую с физическими и юридическими лицами, только с банками. Следовательно, выдавать кредиты или класть деньги на депозиты населению или предприятиям он не может.
2. Банки – это коммерческие организации, главной целью которых является получение прибыли от своей деятельности. Они не производят товаров, банки оказывают финансовые услуги по привлечению и размещению денег.
3. Деньги откуда-то надо брать. Есть несколько источников: кредиты из ЦБ, от других банков, населения или предприятий. Эти источники не бесплатные. За кредиты надо платить проценты, а по депозитам – выплачивать доход вкладчикам.
4. Центробанк выдает кредит банкам минимум под ключевую ставку. Значит, банк не может кредитовать население или предприятия под меньший процент. Разница между ними – это доход банка, который еще надо уменьшить на сумму расходов (создание резервов, текущие затраты на зарплату, обслуживание клиентов, программное обеспечение, безопасность и пр.), чтобы получить чистую прибыль.
5. Коммерческий банк привлекает деньги во вклад под меньший, чем в ЦБ, процент. Ведь эти деньги надо застраховать в АСВ, обслужить их прием и выдачу, заплатить проценты. Поэтому они должны стоить банку дешевле, чем кредит в Центробанке.

Если банк предлагает депозит под процент выше, чем ключевая ставка, это повод повнимательнее к нему присмотреться. Причины такого выгодного предложения могут быть разные:

мошенничество;
близость банкротства и попытка его избежать за счет денег клиентов;
невозможность получения денег в ЦБ;
проблемы с операционной деятельностью;
только что созданный банк пытается привлечь к себе внимание и пр.

Высокие проценты – это повышенные риски для клиентов. Чтобы сориентироваться, какой процент будет считаться высоким, нужно посмотреть на базовый уровень доходности. Его ежемесячно рассчитывает Центробанк по вкладам крупнейших банков. На март 2020 г. составляет:

Рынок облигаций

Для инвестора прогнозы понижения ключевой ставки – это сигнал о том, что скоро повысятся котировки уже обращающихся на рынке облигаций. Это происходит по следующим причинам.

Представим, что Центробанк установил 7,5 %. Значит, предприятия и организации могут привлечь деньги путем размещения долговых ценных бумаг под чуть больший процент. Например, под 8 или 8,5 %. Потом ЦБ снижает ключевую ставку до 6,5. Новые выпуски облигаций уже можно размещать под 7 или 7,5. Эмитенты не хотят переплачивать инвесторам. Цены на бумаги с более высокой доходностью повысятся, ведь они станут привлекательнее по сравнению с новыми выпусками, и спрос со стороны инвесторов увеличится.

Обратная ситуация произойдет, если ключевая ставка будет повышаться.

Штрафы, пени, неустойки

Многие штрафы, пени, неустойки по договорам между юридическими, физическими лицами привязаны к проценту ЦБ, а также штрафы и пени по налогам. Как правило, применяется соотношение 1/300 или 1/150.

Например, при оформлении расписки в документе не всегда прописывается размер процентов в случае невозврата долга. В этом случае кредитор имеет право потребовать их оплатить в размере ключевой ставки.

Налогообложение

От размера процента, установленного ЦБ, зависит величина налога на доходы.

Налогообложение купонов

Корпоративные облигации, доходность которых превышает “ключевая ставка + 5 %” подлежат налогообложению в размере 35 % от превышения.

Пример. Клиент купил облигацию номиналом 1 000 руб. и с купонной доходностью 14,5 % годовых. С превышения в 3,5 % придется заплатить НДФЛ: 1 000 * 3,5 % * 35 % = 12,25 руб.

На повышенный процент по вкладам придется заплатить НДФЛ. Если доходность превысила величину “ключевая ставка + 5 %”, то вкладчик внесет 35 % в бюджет.

Пример. Клиент открыл вклад в банке на 500 тыс. руб. под 12 % годовых. На сегодняшний день необлагаемый лимит составляет: 6 % + 5 % = 11 %. Значит, с превышения надо заплатить НДФЛ:

1. Налогооблагаемая база: 500 000 * (12 % – 11 %) = 5 000 руб.
2. НДФЛ: 5 000 * 35 % = 1 750 руб.

Оплата услуг ЖКХ

За несвоевременную оплату услуг ЖКХ придется заплатить пени, которые тоже зависят от ключевой ставки:

• после одного месяца просрочки (даты оплаты счета по договору с поставщиком услуг) – 1/300 ставки ЦБ, т. е. на февраль 2020 года это 0,02 % за каждый день просрочки;
• после трех месяцев – 1/130, т. е. 0,05 %.

Как рассчитать разные платежи по кредиту

Существует две схемы, по которым рассчитываются займы в банке — аннуитетная и дифференцированная. Первый вариант предусматривает более дорогие кредиты, поскольку процент начисляется на весь объем ссуды. Второй вариант подразумевает процентную ставку по кредиту с учетом предыдущих выплат, поэтому такой заем будет немного дешевле. Можно пересчитать ссуду по двум формулам — аннуитетной и дифференцированной и убедиться в этом лично.

Оформить дифференцированный заем намного сложнее, поскольку банки теряют на этом свой заработок. В том случае, когда это удается, нужно внимательно прочитать договор и убедиться, что отсутствуют дополнительные платежи, которыми кредитор захочет компенсировать потерянные деньги.

Изучая кредитную информацию, заемщикам необходимо внимательно ознакомиться с требованиями и условиями банков. Во время подписания бумаг стоит перечитать все пункты и задать интересующие вопросы по полученному договору. Также стоит перепроверить ежемесячные платежи, размер которых вычисляется по формулам, указанным выше.

Аннуитетные платежи

Аннуитетные платежи подразумевают наличие выплат равными частями на протяжении всего срока кредитования. Обязательный взнос, который необходимо перечислять на счет кредитора, состоит из двух частей — тела и процентов от суммы кредита. Такой способ расчета в интересах банка, поэтому аннуитетные займы предоставляются в большинстве кредитных организаций и имеют оптимальную годовую ставку.

Правильно рассчитать взнос по аннуитетной схеме легче, поскольку весь долг делится на равные части. Определить объемы выплат и сравнить результат с графиком, выданным банком, должен каждый заемщик. Это позволит избежать таких ситуаций, когда клиент погасил весь заем, а некоторая задолженность осталась

Важно мониторить свой счет, платеж сохранять в личном кабинете или распечатывать квитанцию

Дифференцированные платежи

Дифференцированная система кредитования подразумевает изменение ежемесячных выплат в зависимости от остатка долга. Тело займа разделяется на равные части исходя из количества платежей, а процент высчитывается от объема средств, которые остались для погашения. Таким образом, с каждым месяцем кредитные выплаты, которые необходимо осуществить заемщику, уменьшаются.

Кредиторы редко используют дифференцированную систему, поскольку она снижает стоимость займа. Кроме того, при дифференцированном расчете проще погасить долг досрочно, что значит — меньше будет заработок у банковских компаний. Финансовым структурам выгоднее получать стабильный доход в месяц, чем предоставлять недорогое кредитование.

Для подсчета выплат в рамках дифференцированного кредитования лучше использовать таблицу, в которую будет занесена определенная сумма долга каждый месяц на весь срок займа. Какой бы репутацией ни славился банк, необходимо самостоятельно перепроверить график платежей и удостовериться, что нет никаких ошибок.

Вычисление процентов по пропорции

Сейчас мы не будем брать в расчет вычисление процентов с использованием тех же таблиц офисных программ типа Excel, которые делают это в автоматическом режиме при задании соответствующей формулы.

В некоторых случаях используется калькулятор, на котором можно задавать вычисление подобных действий. Но речь сейчас не об этом.

Рассмотрим наиболее распространенные способы вычислений, знакомые нам из школьного курса математики.

Простейшим и самым распространенным способом является решение пропорции.

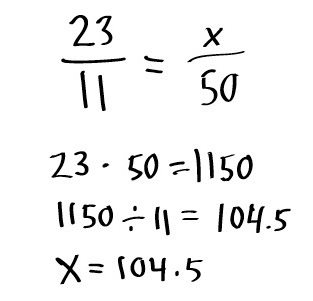
В данном случае исходное число задается в виде 100 процентов (скажем, некое произвольное число «a»), а его часть (допустим, «b») – в виде неизвестной «x». В математике это выглядит так:

Исходя из правил пропорции, можно вычислить неизвестное число x. Для этого используется так называемый перекрестный метод. Иными словами, нужно умножить b на 100 и разделить на a. Точно такое же правило действует, если в случае составления пропорции поменять b и x местами, когда процент известен, а нужно вычислить часть в числовом выражении.

Расчет доли в процентах (удельного веса).

Давайте рассмотрим несколько примеров, которые помогут вам быстро вычислить долю в процентах от общей суммы в Excel для различных наборов данных.

Пример 1. Сумма находится в конце таблицы в определенной ячейке.

Очень распространенный сценарий — это когда у вас есть итог в одной ячейке в конце таблицы. В этом случае формула будет аналогична той, которую мы только что обсудили. С той лишь разницей, что ссылка на ячейку в знаменателе является абсолютной ссылкой (со знаком $). Знак доллара фиксирует ссылку на итоговую ячейку, чтобы она не менялась при копировании формулы по столбцу.

Возьмем данные о продажах шоколада и рассчитаем долю (процент) каждого покупателя в общем итоге продаж. Мы можем использовать следующую формулу для вычисления процентов от общей суммы: 

=G2/$G$13

Вы используете относительную ссылку на ячейку для ячейки G2, потому что хотите, чтобы она изменилась при копировании формулы в другие ячейки столбца G. Но вы вводите $G$13 как абсолютную ссылку, потому что вы хотите оставить знаменатель фиксированным на G13, когда будете копировать формулу до строки 12.

Совет. Чтобы сделать знаменатель абсолютной ссылкой, либо введите знак доллара ($) вручную, либо щелкните ссылку на ячейку в строке формул и нажмите F4.

На скриншоте ниже показаны результаты, возвращаемые формулой. Столбец «Процент к итогу» отформатирован с применением процентного формата.

Пример 2. Часть итоговой суммы находится в нескольких строках.

В приведенном выше примере предположим, что у вас в таблице есть несколько записей для одного и того же товара, и вы хотите знать, какая часть общей суммы приходится на все заказы этого конкретного товара.

В этом случае вы можете использовать функцию СУММЕСЛИ, чтобы сначала сложить все числа, относящиеся к данному товару, а затем разделить это число на общую сумму заказов:

Учитывая, что столбец D содержит все наименования товаров, столбец F перечисляет соответствующие суммы, ячейка I1 содержит наименование, которое нас интересует, а общая сумма находится в ячейке F13, ваш расчет может выглядеть примерно так:

Естественно, вы можете указать название товара прямо в формуле, например:

Но это не совсем правильно, поскольку эту формулу придется часто корректировать. А это затратно по времени и чревато ошибками.

Если вы хотите узнать, какую часть общей суммы составляют несколько различных товаров, сложите результаты, возвращаемые несколькими функциями СУММЕСЛИ, а затем разделите это число на итоговую сумму. Например, по следующей формуле рассчитывается доля черного и супер черного шоколада:

Естественно, текстовые наименования товаров лучше заменить ссылками на соответствующие ячейки.

Для получения дополнительной информации о функции суммирования по условию ознакомьтесь со следующими руководствами:

• Как использовать функцию СУММЕСЛИ в Excel
• СУММЕСЛИМН и СУММЕСЛИ в Excel с несколькими критериями

Аннуитетный платеж

При таком способе погашения кредита заёмщику не надо мудрить – он просто платит каждый месяц одну и ту же сумму. Структура платежа его не интересует, а между тем каждый взнос состоит из двух частей: одна часть гасит основной долг и постепенно увеличивается; вторая часть, которая погашает проценты, естественно, уменьшается.

Это понятие не меняется от того, каким методом мы будем погашать долг:

Осн.плт = См.кредита / Кво.мес

2. Вычислим коэффициент аннуитета

Годовую ставку для удобства расчётов представим в виде десятичной дроби и найдём месячный процент:

Прц.мес = Прц.ст / 12

Формула расчёта коэффициента аннуитета (Коэф.ан) такова:

Коэф.ан = Прц.мес х (1 + Прц.мес)Кво.мес / ((1 + Прц.мес)Кво.мес – 1)

Он зависит только от тела кредита и коэффициента аннауитета:

См.плт = См.кредита х Коэф.ан

4. Вычислим общую сумму долга

Поскольку месячные платежи одинаковы, а количество месяцев известно, то остаётся только перемножить эти величины:

См.общ = См.плт х Кво.мес

Если развернуть формулу для См.плт, то можно общую сумму выразить так:

См.общ = См.кредита х Коэф.ан х Кво.мес

5. Определим переплату

Переплата (См.пп) в чистом виде есть сумма процентов, без учёта комиссии, страховки и проч. Если они есть, то их придётся приплюсовать и к общей сумме, и к переплате.

См.пп = См.общ – См.кредита,

или иначе, если развернуть промежуточные значения:

См.пп = См.кредита х Коэф.ан х Кво.мес – См.кредита = См.кредита х (Коэф.ан х Кво.мес – 1)

Использование процентов на практике

Как рассчитывать проценты, каждый из нас знает еще из школьного курса математики. В повседневной жизни мы сталкиваемся с процентными соотношениями чуть ли не каждую минуту. Любая хозяйка, готовя какое-то блюдо, использует рецептуру, в которой представлено именно процентное соотношение. Самый простой пример: берем полстакана молока… Это и есть математическая трактовка того, что представляет собой определенная часть по отношению к целой.

За основу абсолютно всех вычислений принято считать 100 процентов (100%) или единицу (1), если расчет будет производиться с использованием дробей. От этого и отталкиваются при вычислении какой-либо составляющей от начального показателя.

То же самое касается и вопроса о том, как посчитать процент от суммы, когда в качестве начального (100-процентного) показателя выступает не одно число, а несколько. Вариантов расчета здесь может быть достаточно много. Рассмотрим самые основные.

Обратное вычисление

Очень часто в вопросе о том, как посчитать процент от суммы, возникает и недвусмысленный обратный перевод. На практике это связано, скажем, с обратным вычислением четверти. Всем известно, что этот показатель составляет 25% от начального числа. Пусть, например, цену товара увеличили на 25%, что составило 25 рублей. Нужно найти, сколько стал стоить данный товар. Вот теперь попробуем разобраться, как вычислить не первоначальное число, зная значение процента, а всю сумму, которая должна получиться в конечном итоге. Казалось бы, решение простое:

25 = 25% (1/4 или 0,25);

Нет, абсолютно неверно. Так можно получить только изначальное число, без учета 25%. Для расчета всей суммы с учетом 25% нужно использовать формулу:

Или 100/0,8, что и покажет значение 125 (100 + 25), поскольку 100% плюс 25% в выражении единицы является числом 1,25 (единица плюс четвертая часть), а в обратном виде (1/x) – это именно 0,8. Произведя вычисления, получим, что х = 125.

Заключение

Как видим, ничего особо сложного в том, как посчитать процент от суммы, нет. Правда, в школьной программе обратный перевод почему-то зачастую опускается. Потом у многих бухгалтеров, работающих над отчетами с оплатой того же НДС, очень часто возникают проблемы.

Так что стоит просто учесть основные правила вычисления процентов, и проблемы исчезнут сами собой.

С другой стороны, для удобства можно применять в равной степени как пропорции, так и использование дробей. В первом случае мы имеем, так сказать, классический вариант, а во втором – простое и универсальное решение. Опять же его лучше использовать в случае деления без остатка. Зато при вычислении наиболее популярных долей типа половины, четверти, трети и т. д. такой метод является очень удобным.

Обратные вычисления, как видно из вышеприведенных примеров, тоже чем-то сложным не являются. Главное – учесть обратный коэффициент при расчете искомого числа. Думается, теперь все встало на свои места. Как говорится, простая математика.

Довольно часто перед нами встает такая задача, как посчитать процент от числа. В нашу жизнь прочно вошли такие понятия, как банковские проценты на вклад и кредит.

В выпусках новостей часто говорят о росте ВВП или пенсий на сколько-то процентов. Ребенок просит помочь с задачей, в которой необходимо вычислить процент доли химических элементов. Жизнь заставляет разобраться, что такое процентное отношение и как его считать.

От слова «цент», означающего число «сто», произошло множество известных слов. Сам «цент» — сотая часть доллара, «евроцент» — сотая часть евро. Слово «центнер» означает 100 кг. Знатоки истории вспомнят про центуриона, или сотника, в Древнем Риме.

Процент — слово, имеющее тот же корень, означает сотую часть какого-либо числа. Зачастую приходится сравнивать несколько чисел между собой, определить их соотношение. При этом удобней иметь дело не с целым числом, а какой-то долей.

Причем если все вышеназванные слова описывают зафиксированные величины, то наша величина может означать абсолютно разные вещи.

В каждом отдельном случае процент рассчитывается для конкретной величины и имеет с ней одинаковую размерность.

Например, проценты от некой суммы рублей будут измеряться в рублях. А процентная доля работ, измеряемых в кубометрах, тоже будет составлять сколько-то кубометров.